Geometria iperbolica

Bolyai e Lobacevskij sulla scia di Gauss che per primo si rese conto che una geometria non-euclidea può essere sviluppata con lo stesso rigore e ampiezza della geometria euclidea, costruirono una geometria iperbolica nella quale la somma degli angoli di un triangolo è sempre inferiore a 180°, mentre nella geometria ellittica (Geometria di Riemann) tale somma è sempre maggiore.

Einstein si servì di una rielaborazione della geometria di Riemann per costruire il suo modello relativistico.

2 Geometria ellittica

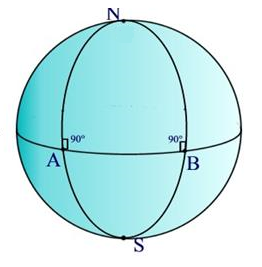
Per avere un'idea della geometria ellittica si immagini un modello costituito da una sfera.

La sfera corrisponde al piano e le rette alle circonferenze ottenute da un piano che taglia la sfera passando per il centro, non diversamente dalla rappresentazione dei meridiani e dei paralleli sul globo terrestre.

È evidente che non esistono rette che non si incontrino: un simile spazio è privo di parallele e non può, ovviamente che porre teoremi diversi da quelli di Euclide, a cominciare dalla somma degli angoli interni di un triangolo.

Prendiamo in considerazione un triangolo con un vertice coincidente con il polo e gli altri due posizionati sull'equatore.

Meridiano ed equatore si incontrano perpendicolarmente formando angoli retti. La somma degli angoli interni da loro formati risulta dunque essere sempre di 180°. Se aggiungiamo l'ampiezza del terzo vertice coincidente con il polo si vede bene che la somma interna degli angoli non può che essere sempre maggiore di 180°.

3 Significato delle geometrie non-euclidee

Le geometrie non euclidee dimostrano che gli assiomi della geometria – la scienza perfetta e assoluta per antonomasia – sono solo ipotesi convenzionali né vere né false.

Non esiste una verità in geometria. Tutte le geometrie hanno una loro validità logica che dipende dalla coerenza intrinseca del linguaggio adottato.

La scelta dell'una o dell'altra dipende dall'uso che se ne intende fare.

La geometria euclidea resta valida nell'applicazione a porzioni “limitate” dello spazio, mentre le geometrie non euclidee servono nella descrizione dello spazio a livello planetario.